| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
Tags
- datatype
- 자료형
- programmers
- 연산자
- Fluent-bit
- Java
- MergeSort
- datastructure
- jvm
- While
- SpringBoot Initializr
- Kotlin
- C++
- redis
- lambda
- quicksort
- IAC
- JPA
- zgc
- UserDetails
- Algorithm
- g1gc
- Class
- Spring Security
- Sprint Security
- For
- 기초
- ansible
- If
- JavaScript
Archives
- Today
- Total
뭐라도 끄적이는 BLOG
Sort - QuickSort 본문
QuickSort는 분할 정복 알고리즘 중 하나이다. 임의의 요소 하나를 pivot으로 선택하고 선택한 pivot을 기준으로 숫자를 분할한다. pivot을 선택하는 방법은 여러 방법이 있다.
- 첫 번째 요소를 pivot으로 선택
- 마지막 요소를 pivot으로 선택
- 임의의 요소를 pivot으로 선택
- 중앙 요소를 pivot으로 선택
배열을 오름차순으로 정렬하는 경우를 예시로 한다.
우선 배열의 한 요소를 pivot으로 선택한다. (그림은 첫 번째 요소를 pivot으로 선택)

이제 pivot을 제외하고 pivot보다 작은 요소를 앞(배열의 작은 인덱스)에 두고 pivot보다 큰 요소를 뒤(배열의 큰 인덱스)로 두어야 한다. 이때 분할된 두 그룹은 정렬되어 있지 않다.
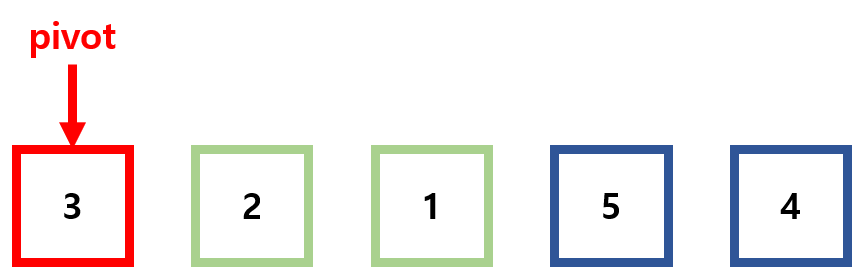
pivot을 작은 값들과 큰 값들의 사이에 놓는다.

그리고 각각의 그룹들이 다시 quick sort과정을 거친다.

QuickSort 과정
QuickSort C Code
첫 번째 구현 방법
void quick_sort(int* arr, int l, int r)
{
if (l >= r)
return;
int pivot, left, right;
int temp;
pivot = l;
left = l + 1;
right = r;
while (left <= right)
{
while(left <= r&& arr[left] <= arr[pivot])
left++;
while(right > l&& arr[right] > arr[pivot])
right--;
if (left <= right)
{
temp = arr[right];
arr[right] = arr[left];
arr[left] = temp;
}
else
{
temp = arr[pivot];
arr[pivot] = arr[right];
arr[right] = temp;
}
}
quick_sort(arr, l, right - 1);
quick_sort(arr, right + 1, r);
}두 번째 구현 방법
void swap(int* a, int* b)
{
int t = *a;
*a = *b;
*b = t;
}
int partition(int arr[], int low, int high)
{
int pivot = arr[high];
int i = low;
for (int j = low; j <= high - 1; j++)
{
if (arr[j] < pivot)
{
swap(&arr[i], &arr[j]);
i++;
}
}
swap(&arr[i], &arr[high]);
return i;
}
void quick_sort2(int arr[], int low, int high)
{
if (low < high)
{
int pivot = partition(arr, low, high);
quick_sort2(arr, low, pivot - 1);
quick_sort2(arr, pivot + 1, high);
}
}QuickSort알고리즘의 특징
장점
- 시간 복잡도가 O(nlog2 n)를 가지는 다른 정렬 알고리즘과 비교했을 때 평균적으로 빠르다.
- O(log n)만큼의 메모리를 사용한다.
단점
- 이미 정렬된 배열에서 가장 첫 번째 또는 마지막 요소를 pivot으로 설정하면 QuickSort의 불균형 분할에 의해 오히려 수행 시간이 더 많이 걸린다. O(n^2)
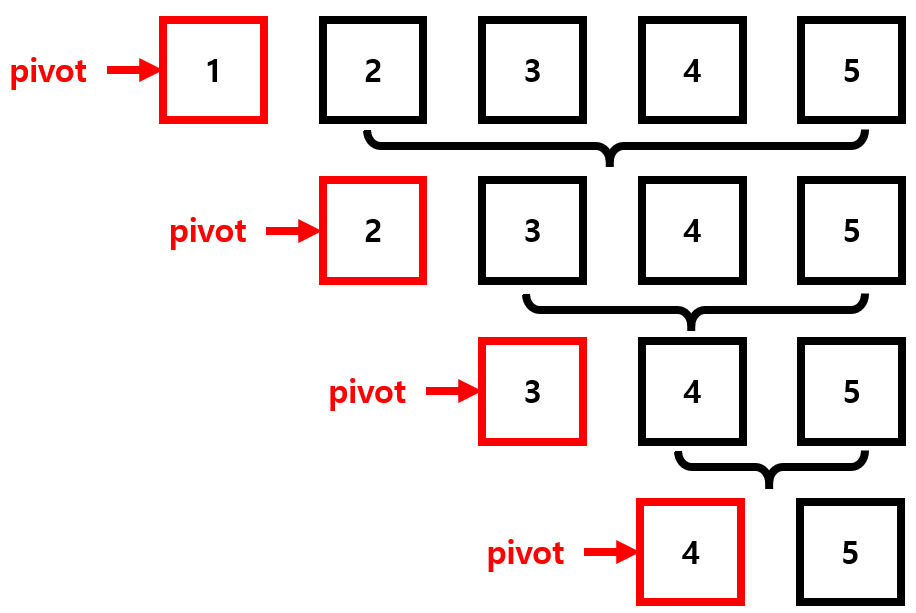
이경우 pivot을 중앙 요소로 지정하면 불균형이 없어진다.
Quick Sort는 평균적인 시간 복잡도는 O(nlog2 n)이다. 최악의 경우는 위와 같이 O(n^2)가 된다.
※참고 자료
반응형
'기본이론 > Algorithm' 카테고리의 다른 글
| Dijkstra Java Code (0) | 2023.07.23 |
|---|---|
| Sort - QuickSort vs MergeSort (0) | 2023.06.18 |
| Sort - MergeSort (0) | 2023.06.18 |
| Algorithm (0) | 2023.06.18 |

