| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- JPA
- While
- zgc
- Kotlin
- 연산자
- For
- redis
- Algorithm
- IAC
- Java
- JavaScript
- g1gc
- Class
- programmers
- Spring Security
- 기초
- datastructure
- MergeSort
- lambda
- jvm
- Sprint Security
- C++
- If
- datatype
- Fluent-bit
- UserDetails
- quicksort
- 자료형
- ansible
- SpringBoot Initializr
- Today
- Total
뭐라도 끄적이는 BLOG
Lec 02 Linear Regression 본문
Regression
Regression(회귀)는 Machine Learning(머신 러닝)에서도 Training Data Set을 사용하는 Supervised Learning의 한 종류 입니다.
Linear Regression

학생이 공부한 시간 x를 입력하여 학생의 시험점수 y를 예측하는 것도 Regression의 한종류라고 할 수 있습니다.
어떤 학생이 공부한 시간(x)당 어떤점수(y)가 나오는지 데이터를 예시로 사용하겠습니다. 예측하고자하는 최종적 목표는 0~100까지 점수입니다. 이렇게 특정 범위를 찾아내는 것이기 때문에 이러한 형태의 머신러닝은 Regression이라고 합니다.
해당 경우는 학생이 공부한 시간이x가 크면 클수록 학생의 시험 성적 y가 높은 경우가 많은것을 볼수 있고 이것은 Linear한 성질을 갖는 그래프형태로 나타낼 수 있기 때문에 Linear Regression이라고 분류할 수 있습니다.
Hypothesis(가설)

Linear Regression에서 학습하기 전에 먼저 Hypothesis(가설)을 세울 필요가 있습니다. 여기서 Hypothesis는 데이터를 표현하는 방정식을 의미하는데 Linear Regression은 직선적 관계를 가지고 있기 때문에 우리가 알고있는 1차방정식 형태로 표현 할 수 있습니다.
H(x) = Wx + b
공부한 시간이 많을수록 성적이 높아진다, 집이 클수록 집값이 높아진다. 등 많은 현상들이 Linear한 성질을 가지고 설명할 수 있기 때문에 Linear Regression은 간단하지만 중요합니다.
이러한 형태중 어떤 선이 가장 좋은 값인지 찾기위해 W와 b값에 변화를 주어야 합니다.
해당 그림에서 3가지 선중 푸른색의 선이 가장 좋은 형태인것이 나타나고 있습니다.
Cost function
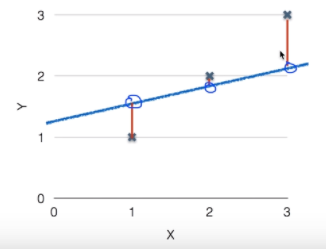
Hypothesis는 입력값 x에서 예측한 값H(x)와 실제값 y간의 거리들을 모두 합한값이 작으면 작을 수록 좋습니다. 이런 거리 값들을 계산할때 사용하는 함수가 Cost Function(비용함수)이며 또다른 이름으로 Loss Function(손실함수)이라고 부르기도 합니다.
해당 그림에서 각 점과 선의 거리를 찾고 그거리가 멀면 안좋고 가까우면 좋은 형태일 것이라는 것을 예상할 수 있습니다.
Cost Function은 모든 x값들에서의 거리를 모두 계산해야 하므로
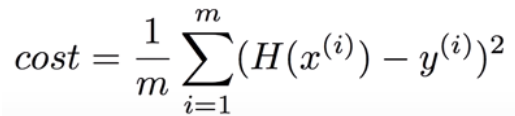
로 표현 할 수 있습니다. 해당 공식에 H(x) = Wx +b를 대입해 보면 Cost Function은 실질적으로 W와 b를 변수로 갖는 함수 라는 것을 알 수 있습니다.
제곱을 한 이유는 차이 값을 일정하게 양수로 표현하게되고 그리고 차이가 클수록 패널티를 더 늘릴수 있는 장점이 있기 때문에 제곱을 해줍니다.
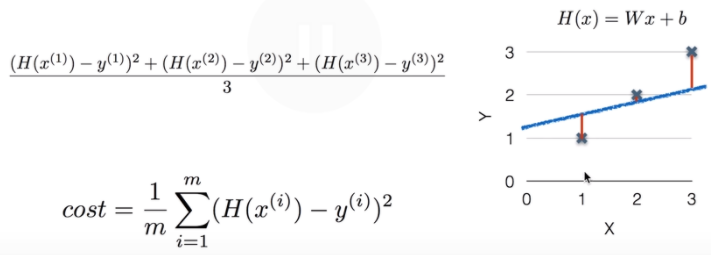
여기서 m은 학습 데이터의 갯수입니다.

Cost function은 결과적으로로 W, b의 function이 됩니다. 이 cost가 가장 작은 값을 가지게 하는 W와 b를 구하는 것이 linear regression의 학습입니다.
학습의 목표 Minimize cost

학습의 목표는 W,b로 cost의 값을 최소로 만드는 것입니다.
모두를 위한 머신러닝/딥러닝 강의
hunkim.github.io
'AI > 모두를 위한 머신러닝' 카테고리의 다른 글
| Lec 06 Softmax Regresion(Multinomial Logistic Regression) (0) | 2021.05.02 |
|---|---|
| Lec 05 Logistic (regression) classification cost function & gradient decent (0) | 2021.04.25 |
| Lec 04 Multivariable linear regression (0) | 2021.04.25 |
| Lec 03 How to minimize cost (0) | 2021.04.25 |
| Lec 01 Machine Leaning (0) | 2021.04.25 |




